Das Volumen eines Parallelepids

Wir zeigen, dass gilt: $$ V = \vec{a} \times \vec{b} \cdot \vec{c} $$

Das Volumen eines Parallelepipeds ist das Produkt der Grundfläche und der zugehörigen Höhe.

Die Grundfläche ist ein Parallelogramm und kann berechnet werden mit Hilfe des Vektorproduktes: $$ A = |\vec{n}| = |\vec{a} \times \vec{b}| $$

Die zu der Fläche zugehörige Höhe ist senkrecht zu der Fläche. Die Höhe hat dieselbe Richtung wie die Normale $\vec{n}|$.

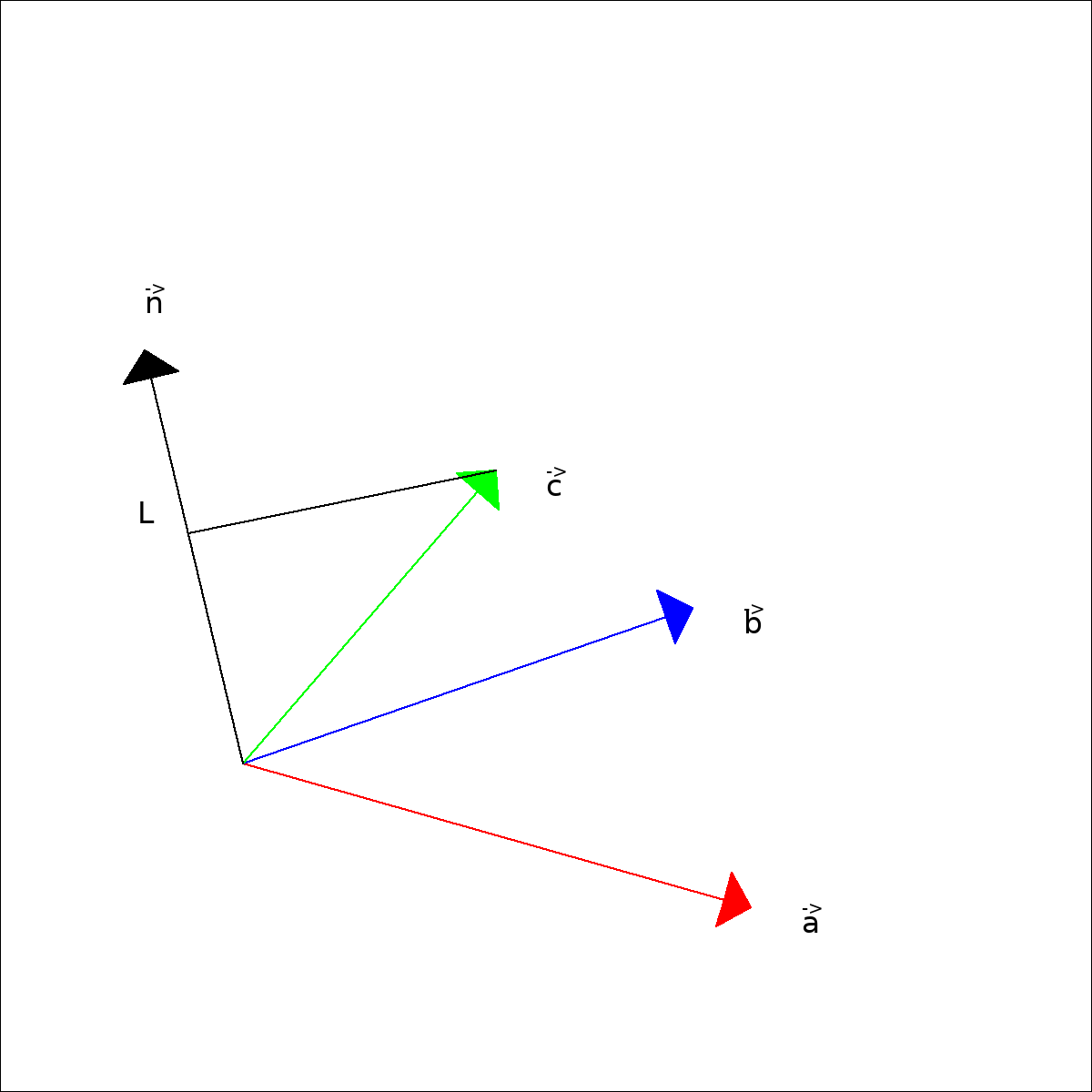
Drei Vektoren — Die beiden Vektoren $\vec{a}$ und $\vec{b}$ bilden die Fläche. Die Höhe erhält man, indem man den Vektor $\vec{c}$ auf die Normale projeziert. L ist der Projektionspunkt des $\vec{c}$ auf der Normalen $\vec{n}$. Maxima Code

L ist der Punkt auf der Normalen, der entsteht, wenn man die Spitze des Vektors $\vec{c}$ auf die Normale projeziert. $ \overrightarrow{0L}$ ist gerade die Höhe auf der Fläche, die durch die beiden Vektoren $\vec{a}$ und $\vec{b}$ gebildet wird.

Das Volumen ist gerade die Multiplikation der Fläche mit der Länge der Projektion auf den Vektor $\vec{n}$: $$ V = \vec{n} \cdot \vec{c} = \vec{a} \times \vec{b} \cdot \vec{c}$$