Abstand zwischen einem Punkt und einer Geraden: Hilfsebene

Gesucht ist der minimale Abstand zwischen einem Punkt und einer Geraden. $$ g: \vec{x} = \vec{a} + t \vec{v} \;\;\; P = \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} $$

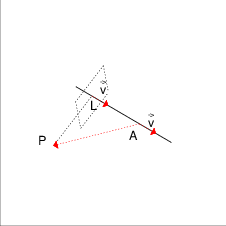
Es gibt eine Ebene, die senkrecht zur Geraden ist und den Punkt P enthält. Da die Ebene senkrecht zur Geraden ist, ist der Schnittpunkt der Ebene mit der Geraden der Lotpunkt L.

Der Richtungsvektor der Geraden ist auch der Normalenvektor der Ebene. Deswegen lässt sich die Normalenform schnell finden: $$ E: \left[ \vec{x} - \vec{p} \right] \cdot \vec{v} = 0 $$

L ist nun der Schnittpunkt der Ebene mit der Geraden. $$ E: \left[ \vec{a} + t \vec{v} - \vec{p} \right] \cdot \vec{v} = 0 $$ Diese Gleichung enthält nur eine Unbekannte: t

Einsetzen ergibt: $$ \begin{array}{rcl} \overrightarrow{LP} \cdot \overrightarrow{v} &=& 0 \\ \overrightarrow{L-P} \cdot \overrightarrow{v} &=& 0 \\ (\overrightarrow{a} + t_l \overrightarrow{v} - \overrightarrow{P}) \cdot \overrightarrow{v} &=& 0 \end{array} $$ Dies ist eine Gleichung mit einer Unbekannten t.

Beispiel

Gesucht ist der minimale Abstand zwischen einem Punkt und einer Geraden. $$ g: \vec{x} = \begin{pmatrix} 13 \\ 12 \\ 7 \end{pmatrix} + t \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} $$ P(2|3|4)

Aufstellen der Hilfsebene: $$ E: \left[ \vec{x} - \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} \right] \cdot \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} = 0 $$

Einsetzen der Geradengleichung und Umformen ergibt: $$ \begin{array}{rcl} \left[ \begin{pmatrix} 13 \\ 12 \\ 7 \end{pmatrix} + t \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} - \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} \right] \cdot \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} &=& 0 \end{array} $$ (Beachten Sie, dass diese Gleichung die Struktur einer Ebenengleichung in Normalenform ist.) $$ \begin{array}{rcl} \overrightarrow{L-P} \cdot \overrightarrow{v} &=& 0 \\ \left[ \begin{pmatrix} 11 \\ 9 \\ 3 \end{pmatrix} + t \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} \right] \cdot \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} &=& 0 \\ (33 + 0 - 3) + (9t + 0t + 1t) &=& 0 \\ 30 + 10t &=& 0 \\ t &=& -3 \end{array} $$

Wir bestimmen den Punkt L: $$ L = \begin{pmatrix} 13 \\ 12 \\ 7 \end{pmatrix} + (-3) \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} = \begin{pmatrix} 4 \\ 12 \\ 10 \end{pmatrix} $$

Der Abstand $$ \begin{array}{rcl} |L-P| &=& \left| \begin{pmatrix} 4 \\ 12 \\ 10 \end{pmatrix} - \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} \right| \\ &=& \left | \begin{pmatrix} 2 \\ 9 \\ 6 \end{pmatrix} \right| \\ &=& \sqrt{2^2 + 9^2 + 6^2} \\ &=& \sqrt{4 + 81 + 36} \\ &=& \sqrt{121} \\ &=& 11 \end{array} $$