Schnittpunkt der Seitenhalbierenden im Dreieck
(Schnittpunkt von Geraden) (Beweis mit Eigenschaften von Vektoren: hier)In diesem Abschnitt beschäftigen wir uns mit dem Schnittpunkt der Seitenhalbierenden eines Dreiecks. Wir werden zwei Eigenschaften beweisen:
- Die Seitenhalbierenden schneiden sich alle in einem gemeinsamen Punkt S.
- Der Punkt S teilt jede Seitenhalbierende im Verhältnis 2:1. Wobei die längere Strecke die Strecke von der Ecke bis zum Punkt S ist.
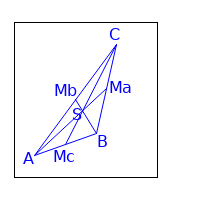
Seitenhalbierende sind Linien im Dreieck. Sie verbinden die Eckpunkte eines Dreiecks mit der Mitte der gegenüberliegenden Seite.
In diesem Beweis werden wir Geradengleichungen benutzen. Der Schnittpunkt der Seitenhalbierenden ist dann der Schnittpunkt der Geraden. Hier gibt es einen anderen Beweis, der nur die Eigenschaften von Vektoren und deren Vielfachen benutzt.
Maxima Code
- Wir erstellen Geradengleichungen, welche die Seitenhalbierenden beinhalten.
- Das Dreieck kann nur durch die beiden Vektoren: $\overrightarrow{AB}$ und $\overrightarrow{AC}$ beschrieben werden. Also werden wir die Geradengleichungen nur mit diesen beiden Vektoren aufstellen.
- Wir ermitteln den Schnittpunkt S von jeweils zwei Geradengleichungen.
- Es wird sich dann herausstellen, dass der Schnittpunkt jeweils gleich ist.
Bestimmen der Geradengleichungen
$$ \begin{array}{rcl} s_a &=& A + r \overrightarrow{AM_a} \\ s_b &=& B + s \overrightarrow{BM_b} \\ s_c &=& C + t \overrightarrow{CM_c} \end{array} $$Die Seitenhalbierenden des Dreiecks sind gerade die Richtungsvektoren unserer Geraden.
Darstellen der Richtungsvektoren durch $\overrightarrow{AB}$ und $\overrightarrow{AC}$
Im Dreieck gilt: $$ \overrightarrow{BC} = \overrightarrow{AC} - \overrightarrow{AB} $$
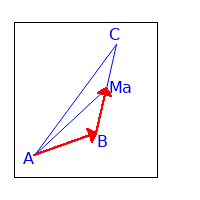
Somit gilt: $$ \begin{array}{rcl} \overrightarrow{AM_a} &=& \overrightarrow{AB} + \frac{1}{2} \overrightarrow{BC} \\ &=& \overrightarrow{AB} + \frac{1}{2} (\overrightarrow{AC} - \overrightarrow{AB}) \\ &=& \frac{1}{2} \overrightarrow{AB} + \frac{1}{2} \overrightarrow{AC} \\ \end{array} $$
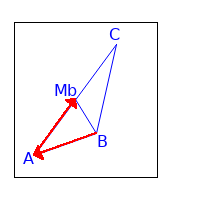
Maxima Code
Maxima Code
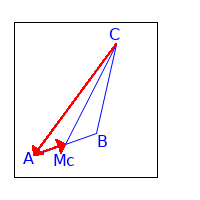
Maxima Code
Damit ergeben sich die Geradengleichungen zu: $$ \begin{array}{rcl} s_a &=& A + \frac{r}{2} (\overrightarrow{AB} + \overrightarrow{AC}) \\ s_b &=& B + s (- \overrightarrow{AB} + \frac{1}{2} \overrightarrow{AC}) \\ s_c &=& C + t (- \overrightarrow{AC} + \frac{1}{2} \overrightarrow{AB}) \end{array} $$
Schnittpunkt von sa und sb berechnen
Wir berechnen den Schnittpunkt, indem wir einen Wert für r und einen Wert für s suchen, so dass beide Geradengleichungen denselben Punkt ergeben. $$ \begin{array}{rcl} s_a &=& s_b \\ A + \frac{r}{2} (\overrightarrow{AB} + \overrightarrow{AC}) &=& B + s (- \overrightarrow{AB} + \frac{1}{2} \overrightarrow{AC} ) \\ A + \frac{r}{2} \overrightarrow{AB} + \frac{r}{2} \overrightarrow{AC} &=& B - s \overrightarrow{AB} + \frac{s}{2} \overrightarrow{AC} \\ \end{array} $$ Jetzt wird sortiert: Terme mit $\overrightarrow{AB}$ nach links und Terme mit $\overrightarrow{AC}$ kommen auf die rechte Seite. $$ \begin{array}{rcl} A + \frac{r}{2} \overrightarrow{AB} + s \overrightarrow{AB} &=& B - \frac{r}{2} \overrightarrow{AC} + \frac{s}{2} \overrightarrow{AC} \\ A + \left( \frac{r}{2} +s \right) \overrightarrow{AB} &=& B + \left( \frac{s}{2} - \frac{r}{2} \right) \overrightarrow{AC} \end{array} $$ $A-B$ ist gerade $- \overrightarrow{AB}$ $$ \begin{array}{rcl} A - B + \left( \frac{r}{2} +s \right) \overrightarrow{AB} &=& \left( \frac{s}{2} - \frac{r}{2} \right) \overrightarrow{AC} \\ - \overrightarrow{AB} + \left( \frac{r}{2} +s \right) \overrightarrow{AB} &=& \left( \frac{s}{2} - \frac{r}{2} \right) \overrightarrow{AC} \\ \left( \frac{r}{2} + s - 1 \right) \overrightarrow{AB} &=& \left( \frac{s}{2} - \frac{r}{2} \right) \overrightarrow{AC} \\ \end{array} $$ Da die Richtungen der Vektoren $\overrightarrow{AB}$ und $\overrightarrow{AC}$ unterschiedlich sind, kann die Gleichung nur dann erfüllt sein, wenn beide Seiten null sind. Dies ergibt zwei Gleichungen:
Einsetzen in sa ergibt: $$ \begin{array}{rcl} S &=& A + \frac{1}{2} r (\overrightarrow{AB} + \overrightarrow{AC}) \\ &=& A + \frac{1}{2} \cdot \frac{2}{3} (\overrightarrow{AB} + \overrightarrow{AC}) \\ &=& A + \frac{1}{3} (\overrightarrow{AB} + \overrightarrow{AC}) \end{array} $$
Schnittpunkt von sa und sc berechnen
Wir berechnen den Schnittpunkt, indem wir einen Wert für r und einen Wert für t suchen, so dass beide Geradengleichungen denselben Punkt ergeben. $$ \begin{array}{rcl} s_a &=& s_c \\ A + \frac{r}{2} (\overrightarrow{AB} + \overrightarrow{AC}) &=& C + t (- \overrightarrow{AC} + \frac{1}{2} \overrightarrow{AB}) \\ A + r \frac{1}{2} \overrightarrow{AB} + r \frac{1}{2} \overrightarrow{AC} &=& C - t\overrightarrow{AC} + \frac{1}{2} t \overrightarrow{AB} \end{array} $$ Jetzt wird wieder sortiert: $$ \begin{array}{rcl} A-C + r \frac{1}{2} \overrightarrow{AC} + t\overrightarrow{AC} &=& \frac{1}{2} t \overrightarrow{AB} - r \frac{1}{2} \overrightarrow{AB} \\ A-C + \left( \frac{r}{2} + t \right) \overrightarrow{AC} &=& \frac{1}{2} (t-r) \overrightarrow{AB} \\ - \overrightarrow{AC} + \left( \frac{r}{2} + t \right) \overrightarrow{AC} &=& \frac{1}{2} (t-r) \overrightarrow{AB} \\ \left( \frac{r}{2} + t - 1 \right) \overrightarrow{AC} &=& \frac{1}{2} (t-r) \overrightarrow{AB} \end{array} $$ Da die Richtungen der Vektoren $\overrightarrow{AB}$ und $\overrightarrow{AC}$ unterschiedlich sind, kann die Gleichung nur dann erfüllt sein, wenn beide Seiten null sind. Dies ergibt zwei Gleichungen:
Einsetzen in sa ergibt: $$ \begin{array}{rcl} S &=& A + \frac{1}{2} r (\overrightarrow{AB} + \overrightarrow{AC}) \\ &=& A + \frac{1}{2} \cdot \frac{2}{3} (\overrightarrow{AB} + \overrightarrow{AC}) \\ &=& A + \frac{1}{3} (\overrightarrow{AB} + \overrightarrow{AC} ) \end{array} $$
Beweisende
Da S der Schnittpunkt von sa und sb und von sa und sc ist, ist S der gemeinsame Schnittpunkt aller drei Seitenhalbierenden.
Darüber hinaus teilt der Punkt S jede Seitenhalbierende im Verhältnis 2:1.

 Koordinatensystem
Koordinatensystem