Abstand zwischen einem Punkt und einer Geraden: Lotpunkt

Gesucht ist der minimale Abstand zwischen einem Punkt und einer Geraden. $$ g: \vec{x} = \vec{a} + t \vec{v} \;\;\; P = \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} $$

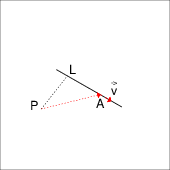
Bei dieser Herleitung nutzen wir die Eigenschaft des Skalarproduktes bei der das Skalarprodukt zweier orthogonaler Vektoren null ergibt.

Die kürzeste Linie von P zur Geraden trifft auf die Gerade senkrecht am Punkt L auf. Die Linie $\overline{LP}$ ist senkrecht zur Geraden und damit senkrecht zum Richtungsvektor: $$ \overrightarrow{LP} \cdot \overrightarrow{v} = 0 $$

Wenn L bekannt wäre, könnte man die Entfernung zwischen den Punkten P und L bestimmen.

L ist ein Punkt der Geraden. D. h., es gibt ein $t_l$ mit: $$ L = \overrightarrow{a} + t_l \overrightarrow{v} $$

Einsetzen ergibt: $$ \begin{array}{rcl} \overrightarrow{LP} \cdot \overrightarrow{v} &=& 0 \\ \overrightarrow{L-P} \cdot \overrightarrow{v} &=& 0 \\ (\overrightarrow{a} + t_l \overrightarrow{v} - \overrightarrow{P}) \cdot \overrightarrow{v} &=& 0 \end{array} $$ Dies ist eine Gleichung mit einer Unbekannten t.

Lösungsformel

Wir vereinfachen in obiger Formel: $$ \overrightarrow{a} - \overrightarrow{P} = \overrightarrow{d} $$ Dann formen wir um und lösen nach den Komponenten auf: $$ \begin{array}{rcl} (\overrightarrow{a} + t \overrightarrow{v} - \overrightarrow{P}) \cdot \overrightarrow{v} &=& 0 \\ (\overrightarrow{d} + t \overrightarrow{v}) \cdot \overrightarrow{v} &=& 0 \\ \overrightarrow{d} \cdot \overrightarrow{v} + t \overrightarrow{v} \cdot \overrightarrow{v} &=& 0 \\ t \overrightarrow{v} \cdot \overrightarrow{v} &=& - \overrightarrow{d} \cdot \overrightarrow{v} \\ t &=& - \, \frac{ \overrightarrow{d} \cdot \overrightarrow{v} }{ \overrightarrow{v} \cdot \overrightarrow{v} } \\ t &=& - \, \frac{ d_1\,v_1 + d_2\,v_2 + d_3\,v_3 }{ v_1^2 + v_2^2 + v_3^2 } \end{array} $$

Beispiel

Gesucht ist der minimale Abstand zwischen einem Punkt und einer Geraden. $$ g: \vec{x} = \begin{pmatrix} 13 \\ 12 \\ 7 \end{pmatrix} + t \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} $$ P(2|3|4)

$$ \begin{array}{rcl} (\overrightarrow{L-P}) \cdot \overrightarrow{v} &=& 0 \\ \left[ \begin{pmatrix} 13 \\ 12 \\ 7 \end{pmatrix} + t \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} - \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} \right] \cdot \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} &=& 0 \end{array} $$ (Beachten Sie, dass diese Gleichung die Struktur einer Ebenengleichung in Normalenform ist.) $$ \begin{array}{rcl} \overrightarrow{L-P} \cdot \overrightarrow{v} &=& 0 \\ \left[ \begin{pmatrix} 11 \\ 9 \\ 3 \end{pmatrix} + t \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} \right] \cdot \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} &=& 0 \\ (33 + 0 - 3) + (9t + 0t + 1t) &=& 0 \\ 30 + 10t &=& 0 \\ t &=& -3 \end{array} $$

Wir bestimmen den Punkt L: $$ L = \begin{pmatrix} 13 \\ 12 \\ 7 \end{pmatrix} + (-3) \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} = \begin{pmatrix} 4 \\ 12 \\ 10 \end{pmatrix} $$

Der Abstand $$ \begin{array}{rcl} |L-P| &=& \left| \begin{pmatrix} 4 \\ 12 \\ 10 \end{pmatrix} - \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} \right| \\ &=& \left | \begin{pmatrix} 2 \\ 9 \\ 6 \end{pmatrix} \right| \\ &=& \sqrt{2^2 + 9^2 + 6^2} \\ &=& \sqrt{4 + 81 + 36} \\ &=& \sqrt{121} \\ &=& 11 \end{array} $$