Lagebeziehungen von Geraden

Zwei Geraden im dreidimensionalem Raum können ...

Zusammenhang mit dem Gaussverfahren

Wenn Sie zwei 3-dimensionale Geraden gleichsetzen erhalten Sie ein Gleichungssystem mit drei Gleichungen. Wenn Sie dann das Gaussverfahren anwenden, können Sie am Ende des Verfahrens ablesen, welche Lage die Geraden zueinander haben.

Übersicht

Schnittpunkt Das Gleichungssystem hat genau eine Lösung.
Identisch Das Gleichungssystem hat unendlich viele Lösungen.
Parallel Das Gleichungssystem hat zwei Nullzeilen in der Matrix. Im Lösungsvektor ist in der Nullzeile keine Null.
Windschief Das Gleichungssystem hat keine Lösung. Für den zweiten Parameter gibt es zwei verschiedene Lösungen.

Parallele Geraden ohne einen gemeinsamen Punkt

$$ g: \vec{x} = \begin{pmatrix} 1\\2\\3 \end{pmatrix} + r \begin{pmatrix} 2\\3\\2 \end{pmatrix} $$ $$ h: \vec{x} = \begin{pmatrix} 1\\2\\4 \end{pmatrix} + s \begin{pmatrix} 4\\6\\4 \end{pmatrix} $$ Die Richtungsvektoren der beiden Geraden g und h sind Vielfache voneinander: $$ 2 \cdot \begin{pmatrix} 2\\3\\2 \end{pmatrix} = \begin{pmatrix} 4\\6\\4 \end{pmatrix} $$ Die Richtungsvektoren zeigen in dieselbe Richtung.

Die beiden Geraden haben entweder alle Punkte gemeinsam oder keinen. $$ \begin{pmatrix} 1\\2\\4 \end{pmatrix} = \begin{pmatrix} 1\\2\\3 \end{pmatrix} + r \begin{pmatrix} 2\\3\\2 \end{pmatrix} $$ Dieses Gleichungssystem hat keine Lösung, denn für die 1. und 2. Zeile muss $r=0$ gelten, für die 3. Zeile muss $r=0{,}5$ gelten.

Wenn man die Geraden gleichsetzt kann man das Gaussverfahren anwenden: $$ \begin{pmatrix} 2 & -4 \\ 3 & -6 \\ 2 & -4 \\ \end{pmatrix} \begin{pmatrix} r \\ s \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} $$ $$ \begin{array}{l} II' = 3 \cdot I - 2 \cdot II \\ III' = III - I \\ \begin{pmatrix} 2 & -4 \\ 0 & 0 \\ 0 & 0 \\ \end{pmatrix} \begin{pmatrix} r \\ s \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \end{array} $$ Da die beiden Spalten Vielfache voneinander sind, erhalten Sie immer zwei Nullzeilen in der Matrix. Da das Gleichungssystem aber keine Lösung haben kann, denn die Geraden haben keinen Schnittpunkt, muss in der zweiten oder in der dritten Zeile im Lösungsvektor eine Zahl ungleich null stehen.

Daraus folgt: Die beiden Geraden sind parallel aber haben keinen gemeinsamen Punkt.

Identische Geraden

$$ g: \vec{x} = \begin{pmatrix} 1\\2\\3 \end{pmatrix} + r \begin{pmatrix} 2\\3\\2 \end{pmatrix} $$ $$ h: \vec{x} = \begin{pmatrix} 3\\5\\5 \end{pmatrix} + s \begin{pmatrix} 2\\3\\2 \end{pmatrix} $$

Die Richtungsvektoren der Geraden g und der Geraden h sind Vielfache von einander. Sie sind sogar identisch.

$$ \begin{pmatrix} 3\\5\\5 \end{pmatrix} = \begin{pmatrix} 1\\2\\3 \end{pmatrix} + r \begin{pmatrix} 2\\3\\2 \end{pmatrix} $$ Diese Gleichung hat eine Lösung für $r=1$.

Die Geraden haben dieselbe Richtung und ein Punkt ist in beiden Geraden enthalten. Daraus folgt, dass die Geraden identisch sind. Wenn man die Geraden gleichsetzt kann man das Gaussverfahren anwenden: $$ \begin{pmatrix} 2 & 2 \\ 3 & 3 \\ 2 & 2 \\ \end{pmatrix} \begin{pmatrix} r \\ s \end{pmatrix} = \begin{pmatrix} 2 \\ 3 \\ 2 \end{pmatrix} $$ $$ \begin{array}{l} II' = 3 \cdot I - 2 \cdot II \\ III' = III - I \\ \begin{pmatrix} 2 & 2 \\ 0 & 0 \\ 0 & 0 \\ \end{pmatrix} \begin{pmatrix} r \\ s \end{pmatrix} = \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix} \end{array} $$ $$ \begin{array}{l} I' = \frac{1}{2} \, \cdot \, I \\ \begin{pmatrix} 1 & 1 \\ 0 & 0 \\ 0 & 0 \\ \end{pmatrix} \begin{pmatrix} r \\ s \end{pmatrix} = \begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix} \end{array} $$ $$ \begin{pmatrix} r \\ s \end{pmatrix} = \begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix} + t \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix} $$ Es gibt unendlich viele Lösungen. Diese bilden ihrerseits wiederum eine Gerade. Diese Lösungsgerade ist identisch mit den beiden gegebenen Geraden.

Geraden mit einem Schnittpunkt

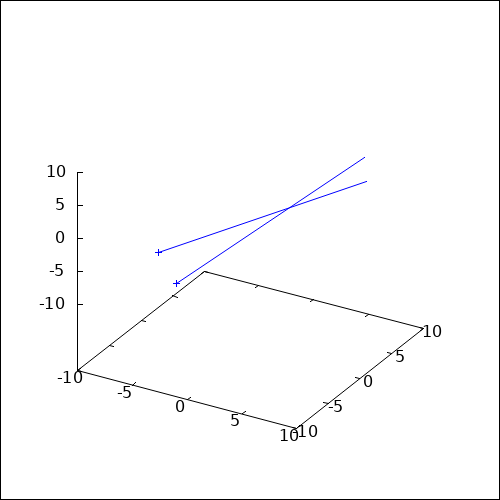
Zwei Geraden im 3-dim. Raum, die sich schneiden.
Zwei Geraden schneiden sich. Maxima Code

Gegeben sind zwei Geraden: $$ g_1: \vec{x} = \begin{pmatrix} 6 \\ 1 \\ 5 \end{pmatrix} + r \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} $$ $$ g_2: \vec{x} = \begin{pmatrix} 7 \\ 3 \\ 8 \end{pmatrix} + s \begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} $$ Gesucht ist der Punkt, der beiden Geraden gemeinsam ist: $$ \begin{pmatrix} 6 \\ 1 \\ 5 \end{pmatrix} + r \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 7 \\ 3 \\ 8 \end{pmatrix} + s \begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} $$ (Achten Sie darauf, dass die Parameter der jeweiligen Geraden unterschiedlich sind. Hier wurde $r$ und $s$ gewählt.) Ziehen Sie auf beiden Seiten $\left(\begin{smallmatrix}6\\1\\5\end{smallmatrix}\right)$ ab: $$ r \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + s \begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} $$ Ziehen Sie auf beiden Seiten $s \left(\begin{smallmatrix}2\\1\\3\end{smallmatrix}\right)$ ab: $$ r \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} - s \begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} $$ Schreiben Sie jetzt, für die Schreibweise beim Gaussverfahren, das Minuszeichen in dem Vektor: $$ r \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} + s \begin{pmatrix} -2 \\ -1 \\ -3 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} $$ Dieses Gleichungssystem lösen Sie mit dem Gaussverfahren: $$ \begin{array}{l} \begin{pmatrix} 1 & -2 \\ 0 & -1 \\ 1 & -3 \end{pmatrix} \cdot \begin{pmatrix} r \\ s \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \end{array} $$ $$ \begin{array}{l} III' = III - I \\ \begin{pmatrix} 1 & -2 \\ 0 & -1 \\ 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} r \\ s \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix} \end{array} $$ $$ \begin{array}{l} III' = III - II \\ \begin{pmatrix} 1 & -2 \\ 0 & -1 \\ 0 & 0 \end{pmatrix} \cdot \begin{pmatrix} r \\ s \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix} \end{array} $$ $$ \begin{array}{l} II' = (-1) \cdot II \\ \begin{pmatrix} 1 & -2 \\ 0 & 1 \\ 0 & 0 \end{pmatrix} \cdot \begin{pmatrix} r \\ s \end{pmatrix} = \begin{pmatrix} 1 \\ -2 \\ 0 \end{pmatrix} \end{array} $$ $$ \begin{array}{l} I' = I + 2 \cdot II \\ \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ 0 & 0 \end{pmatrix} \cdot \begin{pmatrix} r \\ s \end{pmatrix} = \begin{pmatrix} -3 \\ -2 \\ 0 \end{pmatrix} \end{array} $$ Da die untere Zeile nur aus Nullen besteht, gibt es eine eindeutige Lösung für $r$ und $s$. Somit gibt es einen Schnittpunkt. In $g1$ eingesetzt: $$ S = \begin{pmatrix} 6 \\ 1 \\ 5 \end{pmatrix} + (-3) \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} $$ oder in $g2$ eingesetzt: $$ S = \begin{pmatrix} 7 \\ 3 \\ 8 \end{pmatrix} + (-2) \cdot \begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} $$

Windschiefe Geraden

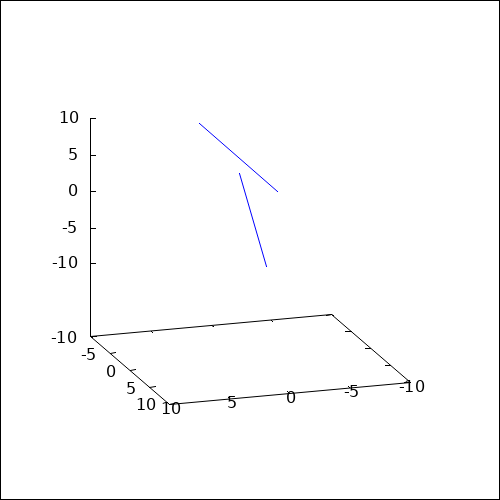
Zwei Geraden im 3-dim. Raum, die sich nicht schneiden.
Zwei Geraden schneiden sich nicht. Maxima Code
Gegeben sind zwei Geraden: $$ g_1: \vec{x} = \begin{pmatrix} 6 \\ 1 \\ 5 \end{pmatrix} + r \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} $$ $$ g_2: \vec{x} = \begin{pmatrix} 7 \\ 3 \\ 8 \end{pmatrix} + s \begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} $$ Wir werden zeigen, dass die beiden Geraden keinen gemeinsamen Punkt haben. Dazu gehen wir genauso vor, als ob wir einen Schnittpunkt suchten. Die Geraden sind aber auch nicht parallel, da die Richtungsvektoren keine Vielfache voneinander sind. $$ \begin{pmatrix} 6 \\ 1 \\ 5 \end{pmatrix} + r \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 7 \\ 3 \\ 8 \end{pmatrix} + s \begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} $$ (Achten Sie darauf, dass die Parameter der jeweiligen Geraden unterschiedlich sind. Hier wurde $r$ und $s$ gewählt.) Ziehen Sie auf beiden Seiten $\left(\begin{smallmatrix}6\\1\\5\end{smallmatrix}\right)$ ab: $$ r \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + s \begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} $$ Ziehen Sie auf beiden Seiten $s \left(\begin{smallmatrix}2\\1\\3\end{smallmatrix}\right)$ ab: $$ r \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} - s \begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} $$ Schreiben Sie jetzt, für die Schreibweise beim Gaussverfahren, das Minuszeichen in dem Vektor: $$ r \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} + s \begin{pmatrix} -2 \\ -1 \\ -3 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} $$ Dieses Gleichungssystem lösen Sie mit dem Gaussverfahren: $$ \begin{array}{l} \begin{pmatrix} 1 & -2 \\ 0 & -1 \\ 0 & -3 \end{pmatrix} \cdot \begin{pmatrix} r \\ s \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \end{array} $$ $$ \begin{array}{l} II' = (-1) \cdot II \\ \begin{pmatrix} 1 & -2 \\ 0 & 1 \\ 0 & -3 \end{pmatrix} \cdot \begin{pmatrix} r \\ s \end{pmatrix} = \begin{pmatrix} 1 \\ -2 \\ 0 \end{pmatrix} \end{array} $$ $$ \begin{array}{l} I' = I + 2 \cdot II \\ \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ 0 & -3 \end{pmatrix} \cdot \begin{pmatrix} r \\ s \end{pmatrix} = \begin{pmatrix} -3 \\ -2 \\ 0 \end{pmatrix} \begin{matrix} \\ \Rightarrow s = -2 \\ \Rightarrow s = 0 \phantom{-} \end{matrix} \end{array} $$

Die Lösung der Gleichung in der zweiten Zeile ergibt $s = -2$. Jedoch die Lösung der Gleichung in der dritten Zeile ergibt $s = 0$.

Somit hat das Gleichungssystem keine Lösung und es gibt keinen gemeinsamen Schnittpunkt und damit sind die Geraden windschief.