Abstand zwischen einem Punkt und einer Geraden: Lotpunkt: Projektion

Gesucht ist der minimale Abstand zwischen einem Punkt und einer Geraden. $$ g: \vec{x} = \vec{a} + t \vec{v} \;\;\; P = \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} $$

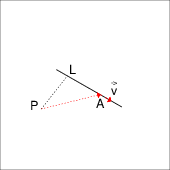
Bei dieser Herleitung nutzen wir die Projektionseigenschaft des Skalarproduktes. Es ergibt sich dieselbe Formel wie bei der Lotpunktberechnung.

Der Lotpunkt L ist die (senkrechte) Projektion des Punktes P auf die Gerade. $|\overline{PL}|$ ist die Entfernung zwischen dem Punkt P und der Geraden, da $\overline{PL}| die kürzeste Strecke zwischen dem Punkt P und einem Punkt der Geraden g ist.

Wir untersuchen zuerst eine Gerade mit einem Richtungsvektor der Länge 1: $$ g:\overrightarrow{x} = A + t \overrightarrow{v_1} $$

$$ \overrightarrow{AP} \cdot \overrightarrow{v_1} = \underbrace{|\overrightarrow{AP}| \cos(\gamma) }_{|\overline{AL}|} \, \underbrace{|\overrightarrow{v_1}|}_{=1} =|\overline{AL}| $$

Diese Länge wird für den Parameter in die Geradengleichung eingesetzt und ergibt L: $$ L = A + \underbrace{\overrightarrow{AP} \cdot \overrightarrow{v_1} }_{\in \mathbb{R}} \, \overrightarrow{v_1} $$

Wenn Sie eine Geradengleichung haben, deren Richtungsvektor nicht die Länge eins hat, so ist das kein Problem. Sie wählen einfach einen neuen Richtungsvektor mit der Länge eins, da es ja nur auf die Richtung ankommt. Teilen Sie Ihren Richtungsvektor durch seine ursprüngliche Länge, dann ist die Länge des neuen Richtungsvektors gerade eins: $$ \overrightarrow{v_1} = \frac{ \overrightarrow{v} }{ |\overrightarrow{v}| } $$

Sie erhalten den Lotpunkt bei einem beliebigen Richtungsvektor durch: $$ L = A + \overrightarrow{AP} \cdot \frac{\overrightarrow{v}}{|\overrightarrow{v}|} \, \frac{\overrightarrow{v}}{|\overrightarrow{v}|} $$ Mit $\overrightarrow{v} \cdot \overrightarrow{v} = |\overrightarrow{v}|^2$ vereinfacht sich die Berechnung des Lotpunktes: $$ L = A + \frac{ \overrightarrow{AP} \cdot \overrightarrow{v} }{ \overrightarrow{v} \cdot \overrightarrow{v} } \, \overrightarrow{v} $$ Beachten Sie, dass der Bruch eine Zahl ist, da jeweils die Skalarprodukte Zahlen ergeben.

Die Entfernung des Punktes P zur Geraden ist dann die Länge $\overline{PL}$

Beispiel

Gesucht ist der minimale Abstand zwischen einem Punkt und einer Geraden. $$ g: \vec{x} = \begin{pmatrix} 13 \\ 12 \\ 7 \end{pmatrix} + t \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} $$ P(2|3|4)

$$

Wir bestimmen den Punkt L: $$ \begin{array}{rcl} L &=& \begin{pmatrix} 13 \\ 12 \\ 7 \end{pmatrix} + \frac{ \begin{pmatrix} -11\\-9\\-3 \end{pmatrix} \cdot \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} }{ \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} \cdot \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} } \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} \\[1cm] &=& \begin{pmatrix} 13 \\ 12 \\ 7 \end{pmatrix} + \frac{ -33 + 3 }{ 10 } \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} \\[0.5cm] &=& \begin{pmatrix} 13 \\ 12 \\ 7 \end{pmatrix} (-3) \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} \\[0.5cm] &=& \begin{pmatrix} 4 \\ 12 \\ 10 \end{pmatrix} \end{array} $$

Der Abstand $$ \begin{array}{rcl} |L-P| &=& \left| \begin{pmatrix} 4 \\ 12 \\ 10 \end{pmatrix} - \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} \right| \\ &=& \left | \begin{pmatrix} 2 \\ 9 \\ 6 \end{pmatrix} \right| \\ &=& \sqrt{2^2 + 9^2 + 6^2} \\ &=& \sqrt{4 + 81 + 36} \\ &=& \sqrt{121} \\ &=& 11 \end{array} $$